Henderson Hasselbalch Equation: Definition. Principle, Applications, and Limitations

The Henderson-Hasselbalch equation provides a general solution to the quantitative treatment of acid-base equilibrium in a biological system. This article explains how to derive the Henderson-Hasselbalch Equation.

Buffers are the mixture of weak acids and their salts of strong bases (or) the mixture of weak bases and their salts of strong acids. Simply put, buffers are an important concept in acid-base chemistry. Buffers help to maintain the normal pH of biological systems. When acid (or) alkali is added, the pH of the solution changes without buffers.

The Henderson Hasselbalch equation is a mathematical equation that calculates the acidity of a solution. Named after English chemist E.J.Henderson, the equation relates the concentration of H+ ions in a solution to its pH. It is also known as the Henderson Hasselbalch equation.

It can be described by:

• In formulae, however, only the coefficients are used to determine a solution’s acidity/base nature, whilst logarithms of these variables (independent of pH) allow for titration reactions in which whole volumes and concentrations of salt(s), bases, or acids may be measured easily over wide ranges; i.e., constant overall resistivity is not required.
• Thus, the Hasselbalch pH can also be used as a measure of salt solubility or acid dissociation constant measured at an arbitrary set of strongly bound ions under laboratory conditions with appropriate instrumentation; and this has led to the widespread adoption of titration chemistry for these purposes in numerous branches (commercial, medical, industrial).

In chemistry and biology, Henderson-Hasselbalch’s equation is used to determine the pH value of a solution.

• In this equation, the pH or pOH of the solution is related to the pKa or pKb of the chemical species involved and the concentration of those species.
• Both the American biologist L.J. Henderson and the Swedish physiologist K.A. Hasselbalch developed it independently to detect blood pH in the bicarbonate buffer system.
• Using kinetic analysis, we have been able for nearly a century to assign acidic intensity changes to acid or base additions or subtractions.
• This equation can be considered as the backbone of acid-base physiology.
• This equation is commonly used to determine the amount of acid and conjugate base needed to prepare a buffer at the desired pH.

Objectives of the Henderson Hasselbalch Equation

The Henderson Hasselbalch equation expresses the relationship between concentration and temperature in terms of a mathematical equation. The equation is named after American chemist Irving Henderson Hasselbalch and was first published in 1918. The equation allows for the determination of the equilibrium constants for a wide range of substances at given temperatures. 

The Henderson Hasselbalch equation’s primary goals are as follows: 

• Calculate the pH, pOH, [H3O+] tot, [OH-] tot, [H3O+] water, and [OH-] water in a solution containing a strong acid (base) given the initial concentration of the acid (base).
• to explain how a buffer solution (either acidic or basic) can withstand significant pH changes when small amounts of acid or base are added to the buffer solution.
• To explain how an acidic or basic buffer solution is made.
• To explain a “buffer solution.”
• To define the term “buffer capacity.”
• Given values of Ka and Kb for conjugate acid-base pairs, determine whether an aqueous solution of salt will be acidic, basic, or neutral.
• To explain how the relative strengths of conjugate acids or bases can be assessed using Kb and Ka values for bases and acids, respectively.
• In a pH seven buffers, determine the protonation state of various biomolecular functional groups.
• To explain how the relative strengths of conjugate acids or bases may be determined using Kb and Ka values for bases and acids, respectively.
• To determine the protonation state of different biomolecule functional groups in pH seven buffers.

Henderson Hasselbalch Equation: Principle/Theory/Derivation

The Henderson Hasselbalch equation is a mathematical formula that allows for the quantitative comparison of two solutions. The equation states that the degree of unsaturation in a solution is equal to the sum of the degrees of saturation of its components.

• According to the Bronsted-Lowry theory of acids and bases, an acid (HA) may give a proton (H+) whereas a base (B) can take one.
• Following the loss of a proton, an acid becomes a conjugate base (A–), while the protonated base becomes a conjugate acid (BH+).
• Regarding the equilibrium equation, acid dissociation is represented as:

HA  ↔       H+  +  A–

• Regarding the equilibrium constant, this connection is as follows:

Buffers act as ‘Shock absorbers” against sudden changes of pH by converting injurious strong acids and bases into harmless weak acid salts.

HA –>  H⁺ + A^–

BA –>  B+ + A^–

If a buffer solution is composed of weak acid HA and its salt, BA, they ionize as follows:

In addition to an alkali, we shall have,

Na⁺ + OH^– + H⁺ + A^–  –>  NaA + H₂O

In addition to the acid,

H⁺Cl^– + B⁺ + A^– —> HA + BCl

Example: Sodium acetate (CH₃COO^–Na⁺) + Acetic acid (CH₃COOH)

Adding strong acid HCl,

C H₃ COOH    +     C H₃ COO^–Na⁺     +     HCl         –>   C H₃ COOH      +      C H₃ COOH     +     NaCl                                                                                                                 (Weak acid)

Adding strong alkali NaOH,

C H₃ COO^– Na⁺    +    C H₃ COOH     +     NaOH –>      C H₃ COO^– Na⁺    +     C H₃ COO^– Na⁺    +    H₂O

Henderson Hasselbalch equation

The pH of a solution containing a weak acid is related to its acid dissociation constant. The relationship can be stated in the convenient form of the “Henderson Hasselbalch equation,” derived below:

A weak acid, HA, ionizes as follows:

HA      –>    H⁺   +    A^–

The equilibrium constant for this dissociation is written as follows:

[H⁺] [A^–]

K=——————

[HA]

Cross multiply:

[H⁺][A^–] = K[HA]

Divide both sides by [A^–]

            [HA]

[H⁺] = K————–

           [A^–]

Take the log of both sides:

                                [HA]

log [H⁺] = log     K —————

                                 [A^–]

                    [HA]

= logK + log ———

                        [A^–]

Multiply through by –1:

                                       [HA]

-log [H⁺] = -log K – log ———-

                                        [A^–]

Substitute pH and for –log [H+] and –logK, respective then:

                    [HA]

P^H= P^K – log ———

                      [A^–]

Then, to remove the minus sign, invert the last term:

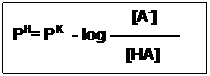
The Handerson-Hasselbalch equation is an expression of great predictive value in protonic equilibrium.

For example,

If the equation is evaluated at several ratios of [A-] / [HA] between the limits of 103 and 10-3 and the calculated pH values are plotted, the result obtained describes the titration curves for a weak acid.

Applications of the Henderson Hasselbalch Equation

1. Calculating the ionized and unionized concentrations of chemicals

For many chemical processes as well as biological systems like enzymes and proteins, knowing the pH of a solution is critical. By knowing the chemical moiety present in the solution, its pKa, and measuring the ratio of its ionized and unionized forms (using some other means), the Henderson Hasselbalch equation may be used to calculate the pH of a solution.

2. Calculating pKa of a molecule using pH

The pKa of a molecule is a significant property of the chemistry of the molecule’s structure. The Henderson-Hasselbalch equation may be used to compute the pKa of a molecule given the chemical moiety present in the solution, the pH of the solution, and the ratio of its ionized and unionized forms (measured using another technique). As a result, this sort of computation necessitates experimental measurements of the molecule’s ionic and anionic forms. Generally, spectroscopic techniques are used to measure the amount of ionized and unionized species.

3. Solubility determination

• The Henderson Hasselbalch equation has been observed to be useful in determining the  pH dependence of solubility.
• Solubility can be determined from its pH, and many components of the solution have a direct relationship with pH.

4. Calculating the isoelectric point of protein

In addition to determining the protein isoelectric point (pH at which proteins do not lose or accept protons), this equation can also be applied to other biological systems.

What Are the Limitations of H-H Equations?

• For this equation to work, it is assumed that the concentrations of acid and their conjugate bases will not change.
• Hydrolysis of water and its effect on the pH of an overall solution are often overlooked.
• It is also assumed to hold true when dealing with strong acids or bases that the base hydrolysis and acid dissociation will not occur.